Constant elasticity of substitution
In economics, Constant elasticity of substitution (CES) is a property of some production functions and utility functions.
More precisely, it refers to a particular type of aggregator function which combines two or more types of consumption, or two or more types of productive inputs into an aggregate quantity. This aggregator function exhibits constant elasticity of substitution.
Contents |
CES production function
The CES production function is a type of production function that displays constant elasticity of substitution. In other words, the production technology has a constant percentage change in factor (e.g. labour and capital) proportions due to a percentage change in marginal rate of technical substitution. The two factor (Capital, Labor) CES production function introduced by Solow [1] and later made popular by Arrow, Chenery, Minhas, and Solow is:[2][3][4]
where
 = Output
= Output = Factor productivity
= Factor productivity = Share parameter
= Share parameter ,
,  = Primary production factors (Capital and Labor)
= Primary production factors (Capital and Labor) =
= 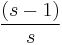
 =
= 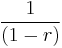 = Elasticity of substitution.
= Elasticity of substitution.
As its name suggests, the CES production function exhibits constant elasticity of substitution between capital and labor. Leontief, linear and Cobb-Douglas production functions are special cases of the CES production function. That is, in the limit as  approaches 1, we get the Cobb-Douglas function; as
approaches 1, we get the Cobb-Douglas function; as  approaches positive infinity we get the linear (perfect substitutes) function; and for
approaches positive infinity we get the linear (perfect substitutes) function; and for  approaching 0, we get the Leontief (perfect complements) function. The general form of the CES production function is:
approaching 0, we get the Leontief (perfect complements) function. The general form of the CES production function is:
where
 = Output
= Output = Factor productivity
= Factor productivity = Share parameter
= Share parameter = Production factors (i = 1,2...n)
= Production factors (i = 1,2...n) = Elasticity of substitution.
= Elasticity of substitution.
Extending the CES (Solow) form to accommodate multiple factors of production creates some problems, however. There is no completely general way to do this. Uzawa [5] showed the only possible n-factor production functions (n>2) with constant partial elasticities of substitution require either that all elasticities between pairs of factors be identical, or if any differ, these all must equal each other and all remaining elasticities must be unity. This is true for any production function. This means the use of the CES form for more than 2 factors will generally mean that there is not constant elasticity of substitution among all factors.
Nested CES functions are commonly found in partial/general equilibrium models. Different nests (levels) allow for the introduction of the appropriate elasticity of substitution.
The CES is a neoclassical production function.
CES utility function
The same functional form arises as a utility function in consumer theory. For example, if there exist  types of consumption goods
types of consumption goods 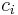 , then aggregate consumption
, then aggregate consumption  could be defined using the CES aggregator:
could be defined using the CES aggregator:
Here again, the coefficients 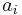 are share parameters, and
are share parameters, and  is the elasticity of substitution. Therefore the consumption goods
is the elasticity of substitution. Therefore the consumption goods 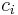 are perfect substitutes when
are perfect substitutes when  approaches infinity and perfect complements when
approaches infinity and perfect complements when  approaches zero. The CES aggregator is also sometimes called the Armington aggregator, which was discussed by Armington (1969).[6]
approaches zero. The CES aggregator is also sometimes called the Armington aggregator, which was discussed by Armington (1969).[6]
A CES utility function is one of the cases considered by Avinash Dixit and Joseph Stiglitz in their study of optimal product diversity in a context of monopolistic competition.[7]
References
- ^ Solow, R.M (1956). "A contribution to the theory of economic growth". The Quarterly Journal of Economics 70: 65–94.
- ^ Arrow, K. J.; Chenery, H. B.; Minhas, B. S.; Solow, R. M. (1961). "Capital-labor substitution and economic efficiency". Review of Economics and Statistics (The MIT Press) 43 (3): 225–250. doi:10.2307/1927286. JSTOR 1927286.
- ^ Jorgensen, Dale W. (2000). Econometrics, vol. 1: Econometric Modelling of Producer Behavior. Cambridge, MA: MIT Press. p. 2. ISBN 0262100827.
- ^ Klump, R; McAdam, P; Willman, A. (2007). "Factor Substitution and Factor Augmenting Technical Progress in the US: A Normalized Supply-Side System Approach". Review of Economics and Statistics (The MIT Press) 89 (1): 183–192.
- ^ Uzawa, H (1962). "Production functions with constant elasticities of substitution". Review of Economic Studies 9: 291–299.
- ^ Armington, P. S. (1969). "A theory of demand for products distinguished by place of production". IMF Staff Papers 16: 159–178.
- ^ Dixit, Avinash; Stiglitz, Joseph (1977). "Monopolistic Competition and Optimum Product Diversity". American Economic Review (American Economic Association) 67 (3): 297–308. JSTOR 1831401.
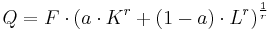
![Q = F \cdot \left[\sum_{i=1}^n a_{i}^{\frac{1}{s}}X_{i}^{\frac{(s-1)}{s}}\ \right]^{\frac{s}{(s-1)}}](/2012-wikipedia_en_all_nopic_01_2012/I/1a422fa0260bd86bdf2899b4605e5571.png)
![C = \left[\sum_{i=1}^n a_{i}^{\frac{1}{s}}c_{i}^{\frac{(s-1)}{s}}\ \right]^{\frac{s}{(s-1)}}](/2012-wikipedia_en_all_nopic_01_2012/I/df2ac100e5c75bab054cdedc7806dcbf.png)